시작하기 전에..
HashMap은 삽입과 조회를 모두 O(1)의 시간에 제공해줍니다.
이러한 특성 때문에 HashMap은 가장 자주 사용되는 자료구조 중 하나인 것 같습니다.
HashMap은 어떤 방법으로 이러한 시간복잡도를 제공해주는지 이해하고 싶어 내부 구조를 파헤쳐 봤습니다.
아래 내용은 HashMap의 내부 구조를 파헤치면서 배운 점과 고민했던 생각을 정리한 글입니다.
'Java를 설계한 사람들이 왜 이렇게 만들었을까?'에 대한 제 대답이 많이 들어있습니다.
공식적인 내용이 아니거나 잘못된 내용이 있을 수도 있다는 점에 유의해 주세요.
목차
- HashMap의 핵심 아이디어에 대해서
- hash collision이 발생하면 어떤 일이 생길까?
- HashMap의 loadFactor에 대해서
- 31이라는 매직 넘버는 왜 이렇게 자주 등장할까?
1. HashMap의 핵심 아이디어에 대해서
HashMap에서 가장 중요한 역할을 하는 함수는 hash()이다.
hash()는 삽입, 조회, 수정, 삭제 연산 모두에서 사용된다.
hash()메서드가 하는 역할은 무엇일까?

HashMap은 객체를 저장할 때, 해당 객체의 고유 번호를 통해 어떤 방(bucket)으로 보낼지를 결정한다.
객체를 가져오는 시점에, 해당하는 방만 확인하여 후보군을 줄이는 것이 핵심이다.
hash()는 객체의 번호를 생성해주는 함수이다. hash는 int를 반환하는데, 이는 약 21억까지의 수를 나타낼 수 있는 자료형이다.
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}그럼 HashMap은 21억개의 방을 미리 만들어놓을까?
그렇지 않다. 실제로 HashMap은 그보다 훨씬 적은 수의 방만 유지하고 하나의 방에 여러개의 객체를 저장한다.
(더 자세히는 아래에서 loadFactor에 대해 다룰 때 논의하겠습니다.)
결국 객체가 가지고 있는 hash라는 번호를 bucket의 크기에 맞게 변환할 필요가 있다.
무작위 숫자를 특정 크기 이하의 숫자로 균등하게 나누는 가장 간단한 아이디어는 나머지 연산이다.
나누기 후 나머지 값은 언제나 0 ~ bucket size - 1이 된다.
예를 들어 bucket size가 10이라고 가정하면 N에 따른 나머지는 아래와 같다.
| N | bucket_size | 나머지 |
|---|---|---|
| 11 | 10 | 1 |
| 14 | 10 | 4 |
| 17 | 10 | 7 |
| 29 | 10 | 9 |
| 25 | 10 | 5 |
| 12245 | 10 | 5 |
정리하자면, hash()는 객체의 번호를 생성하는 함수이다.
HashMap은 객체 번호를 통해 어떤 bucket에 할당할지를 결정한다.
이때, bucket의 수가 무작정 클 수는 없기에 HashMap은 32bit 정수를 bucket의 index로 변환하기 위해 나머지 연산을 이용한다.
해당하는 bucket만 탐색하면 되므로 후보군을 간단히 줄일 수 있어 빠른 연산이 보장된다.
1-1. false positive관점에서 생각해보기
false positive란 결과가 긍정이지만 가짜인 경우를 말한다.
여기선, hash값이 같더라도(positive) 실제로 같은 값은 아닐 수 있다(false)는 뜻이다.
컴퓨터 공학에서는 종종 이런 false positive를 허용하여 성능 향상을 꾀하는 경우가 종종 보인다.
대표적으로 Bloom filter, 주민번호와 카드번호의 check sum과 같은 것이 있다.
사실, 주민번호 check sum의 경우 2020년 10월 이후부터는 규칙이 바뀌어 더이상 check sum으로 검증이 어렵다고 한다.
다만, 가장 간단히 이해할 수 있는 check sum 체계이므로 아래에서는 이전에 쓰이던 방식을 그대로 설명했다.
주민번호 checksum 알고리즘에 대해서 정확히 이해가 가지 않는다면 다른 글을 찾아보라.
이 게시물에서는 다른 숫자를 지지고 볶아서 마지막 숫자와 비교한다는 것만 이해하면 된다.
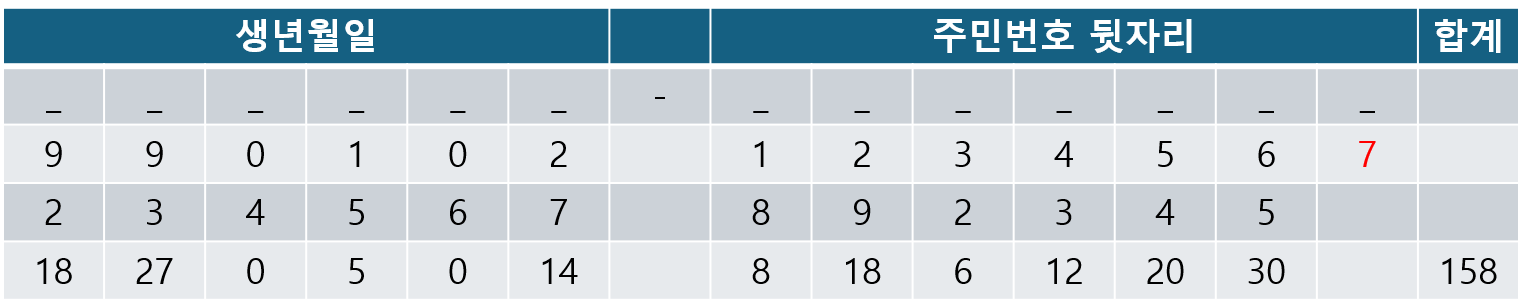
주민번호 맨 뒷자리 숫자는 검증을 위한 숫자이다.
주민번호 앞자리부터 2~9, 다시 2~5를 각 자리수에 곱하여 합을 구한다.(예시에서는 158)
11 - (합(158) mod 11) = 검증 digit 을 만족하는지 확인한다.
예시에서는, 158 mod 11 = 4, 11 - 4 = 7로 마지막 숫자와 일치하는 것을 알 수 있다.

위 알고리즘의 결과가 같다고 해서 반드시 해당 사람의 주민번호가 맞는 것은 아니다.
오타가 있었지만 우연히 checksum digit과 일치하여 success로 넘어가는 경우가 있을 수는 있다.(false positive)
하지만, 생각해보면 확률적으로 대부분의 오타(잘못된 입력)는 check sum에 의해 걸러질 것을 예상할 수 있을것이다.
checksum 알고리즘은 매우 가벼운 연산이다. 반면, 외부 API를 호출해서 검증하는 것은 비교적 매우 무거운 연산이다.
checksum 연산을 통해 대부분의 잘못된 입력을 필터링하고 무거운 연산을 줄이겠다는 논리가 위의 방식이다.
다시, HashMap으로 돌아와 생각해보자.

HashMap에서 데이터를 삽입하는 연산이다.
빨간 네모로 표시한 부분에만 집중하자.
연산은 두가지 부분으로 나뉜다.
1. 기존저장된 객체.hash == 입력된 hash
2. 기존 저장된 객체.key == 입력된 key || 입력된 key.equals(기존 저장된 객체 key)
&&는 early evaluation을 제공해주기 때문에 1번에서 false가 나올 경우 뒤의 연산을 진행하지 않는다.
2번은 key의 동일성을 확인한 뒤 동일하지 않다면 동등성을 equals를 통해 검증한다.
| hash의 값이 같으면 같은 객체인가? | X |
| hash의 값이 다르면 다른 객체인가? | O |
hash를 통해 비교하는 것과 equals를 통해 비교하는 것 중에서 hash가 훨씬 더 빠르다.
이는 hash는 단순히 int값의 비교인 반면, equals는 모든 필드의 값을 하나씩 비교해야하기 때문이다.
또한, hash값이 같다고 해서 같은 객체는 아니다. 하지만 hash값이 다르면 100% 다른 객체이다.
이를 고려할 때, HashMap의 동작 방식 또한 false positive를 허용하여 성능을 향상시킨 사례로 해석할 수 있다.
hash값을 통해 index를 찾아가므로 대부분의 후보군을 필터링할 수 있다.
bucket내에서도 hash를 비교하여 hash값이 다른 경우 equals연산을 하지 않는다.
hash값이 같을 경우 equals()를 통해 한번더 검증이 필요하다.
equals()라는 무거운 작업을 hash()라고하는 가벼운 작업을 통해 대부분 필터링할 수 있다는 관점에서 checksum과 유사한 아이디어로 성능 향상을 이룬 케이스로 볼 수 있을 것이다.
hash비교가 equals()보다 빠르다고?
HashMap에 대해 찾아볼 때, hash값 비교가 equals보다 빠르다는 말을 종종 찾을 수 있었다.
hash를 계산하기 위해서는 모든 필드를 순회하며 연산을 해야하는데 어떻게 equals보다 빠를수가 있을까?
이는, hash값을 비교할 때 매번 hashCode()를 계산하는 것이 아니라 최초 1회 호출한 값을 저장해놓고 사용하기 때문이다.

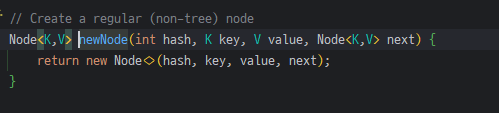
요소가 저장될 때, Node객체가 생성되며 hash값을 필드로 가진다.
따라서 새로운 요소가 들어와 비교가 이뤄질 때, 기존 저장된 요소들은 다시 hashCode()를 호출할 필요가 없다.
새로 입력되는 요소도 마찬가지다. 최초 1회만 hash()가 계산하고 매개변수로 넘어가 재활용된다.

equals()는 매번 호출되어야 하는 반면에 hash값은 한번만 호출되고나면 결과 값을 재활용 할 수 있기에
hash비교는 단순 int의 비교일 뿐이다.
1-2. 나머지 연산을 &로 대신하기

빨간색 네모친 tab[(n-1) & hash]에 주목하자.
n은 bucket의 개수를 의미하며 bucket의 크기는 항상 2^n꼴을 만족한다.
(이는 아래 LoadFactor에 대한 section에서 자세히 설명한다.)
n이 항상 2^n 꼴이라는 점 때문에 나머지 연산을 &로 구현할 수 있다.
n=16, hash = 255라 가정하고 연산을 바라보면 아래와 같은 꼴을 띈다.

결국 하위 n-1개의 bit만 남김으로써 0 ~ 2^n -1까지의 값만 반환된다.
결국 나머지 연산과 똑같은 역할을 &를 통해 할 수 있는 것이다.
나머지 연산은 cpu에서 여러 사이클이 필요한 반면 &는 한 사이클 내에 처리될 수 있는 연산이라 한다.
CPU에서의 동작 방식에 대해서는 다른 포스팅에서 다뤄 보고자 한다.
* 그림의 가독성을 위해 32bit가 아닌 16bit만 표현했다.
1-3. hash()의 내부 구현은 왜 이런 행위를 하고있는걸까?
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
실제 HashMap의 hash()메서드를 보면 생각보다 복잡해 보인다.
1. key == null 이면 0 반환
2. key의 hashCode와 hashCode를 bit right shift 16한 값을 XOR연산하여 반환.
1번은 쉽게 납득이 가지만 2번이 쉽사리 이해가지 않는다.
저 행위가 HashMap에 어떤 영향을 끼치는 걸까?
결론은, 무의미해지는 bit를 최소화 하기 위한 노력으로 생각한다. 아래 예시를 생각해보자.

두 hash값의 상위 16bit는 정 반대의 bit를 가진다. 하지만, (n-1) & hash의 결과는 둘 모두 같다.
상위 높은 bit는 나머지 연산에서 아무런 영향을 끼치지 못한다. 즉 무의미한 bit일 뿐이다.
java의 설계자는 균등하게 index에 분배되도록 하기위해 양 쪽 bit를 섞어주는 연산을 수행하고 싶었던 게 이닐까 싶다.
실제로 bit right shift연산을 수행하면 두 hash값은 아래처럼 변한다.
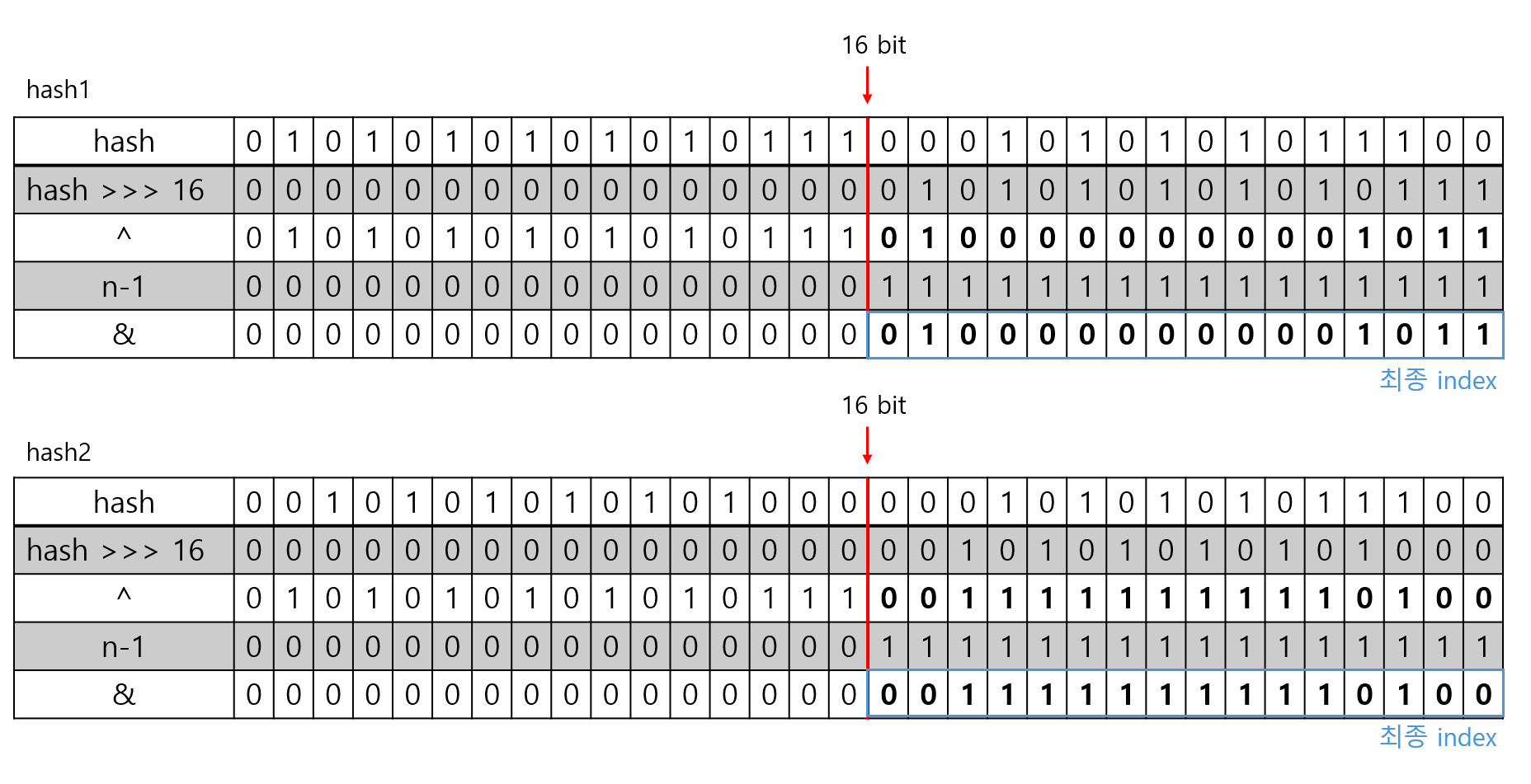
hash1과 hash2는 최종 index값이 전혀 다른 값으로 변하게 된다.
그럼 왜 하필 XOR이였을까?
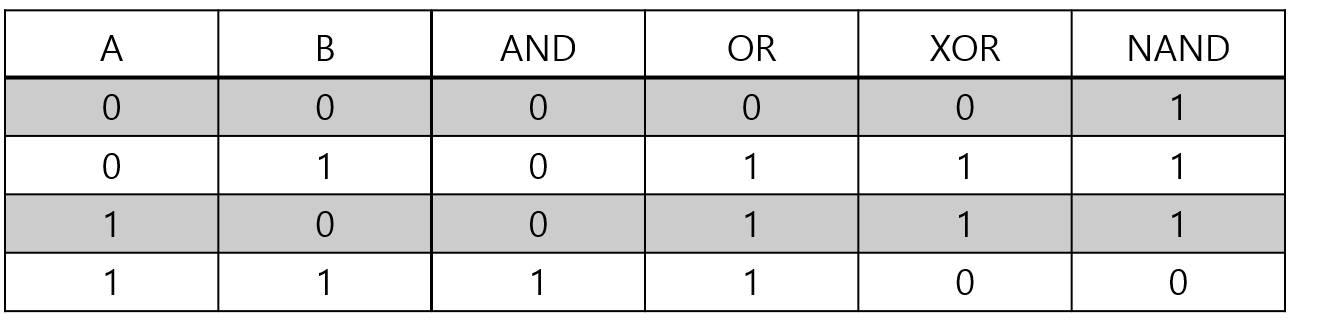
위 표는 A,B의 각 경우의 수에 대해서 논리연산자들의 결과를 나타낸 표이다.
여기서 0과 1의 비율에 주목해보자.

오직 XOR연산만 0과 1의 비율이 1:1로 나타남을 알 수 있다.
index가 균등하게 분배되기 위해서는 논리연산이 bit의 경향성에 영향을 주어서는 안된다.
bit를 균등하게 분배하기 위해 XOR이 사용된 것이 아닐까 생각한다.
1-4. HashMap의 전체적인 그림 정리
결국 INPUT으로 들어온 값을 읽고 쓰기 위해서는 해당 위치를 찾아 가야한다.
아래 그림은 해당 과정을 간략히 나타낸 그림이다.

2. Hash Collsion이 발생하면 어떤 일이 생길까?
자료구조 HashTable에서 Hash Collision에 대처하는 여러가지 전략들이 존재한다.
여기서는 자바가 채택하고 있는 Seperate Chaining방식만 다루려 한다.
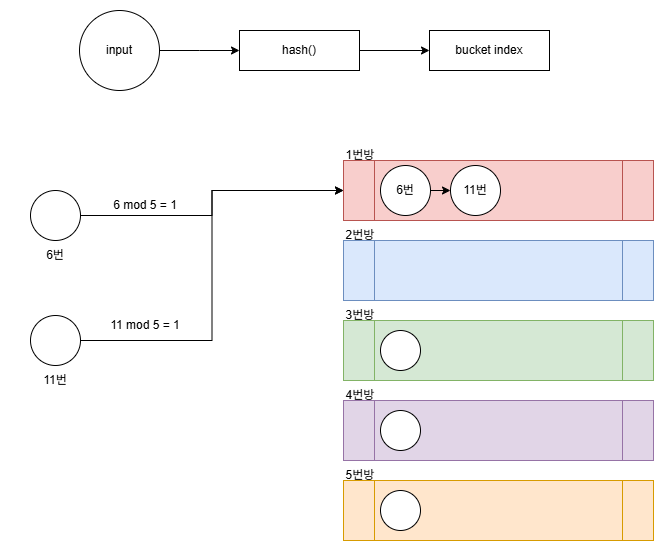
bucket의 크기가 5라 가정할 때, 아래 경우를 생각해보자.

나머지 연산이기에, hash()값이 6, 11은 모두 1번 bucket에 저장되어야 한다.
HashMap의 Bucket은 Linked List로 구현되어 있기에 둘 모두를 1번방에 넣게된다.
2-1. hash Collision이 반복되면 더 이상 O(1)의 시간복잡도가 보장되지 않는 거 아닌가?
HashMap은 O(1)의 시간복잡도를 기대하기에 사용한다.
하지만, 위 설명대로면 O(1)의 시간복잡도를 보장하지 못한다는 생각이든다.
1번 버킷에서 hash Collision이 발생한 요소가 N개라면 1번 버킷을 탐색하는데 O(N)의 시간복잡도가 들것이다.
Java 개발자들은 2가지 방법으로 해당 문제를 보완했다.
1. red-black tree
2. rehashing
여기서는 red-black tree 에 대해서만 다루고 rehashing은 section3에서 자세히 설명한다.

5번방에서 hash collision이 계속 발생해서 많은 요소가 5번 bucket에 삽입되었다고 하자.
이때, 버킷의 시간복잡도는 O(N)일 것이다.
이때, 성능을 끌어 올리기위해 HashMap에서는 bucket을 LinkedList에서 red-black tree로 변환한다.
red-black tree는 조회, 삽입, 수정, 삭제 모두 O(logN)을 보장한다.
언제 Red-Black Tree로 변환되는데?
LinkedList에서 Red-Black Tree로 변환되는 기준이 존재해야한다.
LinkedList에서 Red-Black Tree로 변환되는 역치를 TREEFY_THRESHOLD라고 부른다.
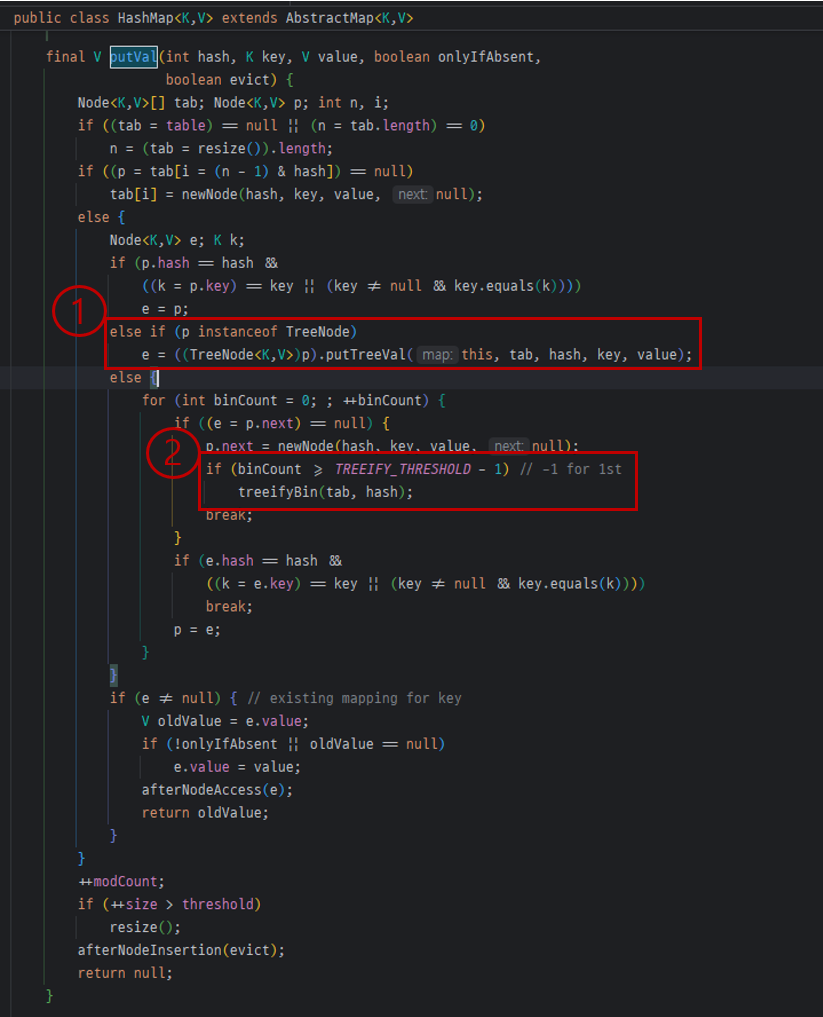
해당 코드는 HashMap에 데이터가 삽입될 때, 동작하는 함수이다.
1번 박스를 보면, bucket이 LinkedList가 아닌 Tree인 경우, tree에 요소를 추가하는 것을 볼 수 있다.
2번 박스를 보면, TREEFY_THRESHOLD역치를 초과하는 시점에 bucket을 tree로 변환하는 것을 볼 수 있다.
근본적인 해결은 아니지 않나?
HashMap은 O(1)의 시간복잡도를 기대한다.
Red-Black Tree로 변경하더라도, 이는 O(logN)의 시간복잡도일 뿐, O(1)의 시간복잡도는 아니다.
단순하게 Red-Black Tree로 변경하는 것은 완전한 해결책은 아니다.
이를 보완하기 위한 해결책이 Rehashing이다.
3. HashMap의 Rehashing
bucket이 LinkedList에서 Red-Black Tree로 바뀌더라도 O(logN)의 시간복잡도이다.
속도를 더 올리기 위해서는 bucket에 많은 요소가 안들어가도록 신경쓰는 것이 중요하다.
이를 위해서는 hash()함수가 균등하게 잘 분배되도록 고려해야겠지만 bucket의 수에 비해 너무 많은 요소가 삽입될 경우 다량의 hash collsion은 불가피하다.
HashMap은 요소가 삽입됨에 따라 어느 시점에 bucket의 크기를 늘리는 로직이 존재한다.
이때 고려할 것은 요소를 삽입할 때, bucket_size를 이용해 나머지 연산으로 bucket의 위치를 결정했다는 것이다.
때문에 bucket 크기가 늘어날 때 기존 요소들도 재배치 되어야 하며 이를 rehashing이라 부른다.
3-1. HashMap의 Load Factor
일정 개수이상의 요소가 HashMap에 삽입될 때, bucket 수를 증가시키는 기준이 loadFactor이다.

HashMap 내부를 보면 threshold와 loadFactor가 존재한다. 아래 예시를 살펴보자.
| capacity | loadFactor | threshold | 재배치 |
| 16 | 0.75 | 12 | 13번째 원소가 삽입될 때, 재배치 |
| 32 | 0.75 | 24 | 25번째 원소가 삽입될 때, 재배치 |
| 64 | 0.75 | 48 | 49번째 원소가 삽입될 때, 재배치 |
| 128 | 0.75 | 96 | 97번째 원소가 삽입될 때, 재배치 |
default initial capacity는 16이다.
load factor는 capacity의 몇%가 찼을 때 재배치가 이루어질 지를 저장하는 필드이다.
threshold는 capacity * loadFactor의 결과값을 저장하고 있다.
아래는 실제 resize()메서드 원문이다.
final Node<K,V>[] resize() {
Node<K,V>[] oldTab = table;
int oldCap = (oldTab == null) ? 0 : oldTab.length;
int oldThr = threshold;
int newCap, newThr = 0;
if (oldCap > 0) {
if (oldCap >= MAXIMUM_CAPACITY) {
threshold = Integer.MAX_VALUE;
return oldTab;
}
else if ((newCap = oldCap << 1) < MAXIMUM_CAPACITY &&
oldCap >= DEFAULT_INITIAL_CAPACITY)
newThr = oldThr << 1; // double threshold
}
else if (oldThr > 0) // initial capacity was placed in threshold
newCap = oldThr;
else { // zero initial threshold signifies using defaults
newCap = DEFAULT_INITIAL_CAPACITY;
newThr = (int)(DEFAULT_LOAD_FACTOR * DEFAULT_INITIAL_CAPACITY);
}
if (newThr == 0) {
float ft = (float)newCap * loadFactor;
newThr = (newCap < MAXIMUM_CAPACITY && ft < (float)MAXIMUM_CAPACITY ?
(int)ft : Integer.MAX_VALUE);
}
threshold = newThr;
@SuppressWarnings({"rawtypes","unchecked"})
Node<K,V>[] newTab = (Node<K,V>[])new Node[newCap];
table = newTab;
if (oldTab != null) {
for (int j = 0; j < oldCap; ++j) {
Node<K,V> e;
if ((e = oldTab[j]) != null) {
oldTab[j] = null;
if (e.next == null)
newTab[e.hash & (newCap - 1)] = e;
else if (e instanceof TreeNode)
((TreeNode<K,V>)e).split(this, newTab, j, oldCap);
else { // preserve order
Node<K,V> loHead = null, loTail = null;
Node<K,V> hiHead = null, hiTail = null;
Node<K,V> next;
do {
next = e.next;
if ((e.hash & oldCap) == 0) {
if (loTail == null)
loHead = e;
else
loTail.next = e;
loTail = e;
}
else {
if (hiTail == null)
hiHead = e;
else
hiTail.next = e;
hiTail = e;
}
} while ((e = next) != null);
if (loTail != null) {
loTail.next = null;
newTab[j] = loHead;
}
if (hiTail != null) {
hiTail.next = null;
newTab[j + oldCap] = hiHead;
}
}
}
}
}
return newTab;
}
resize()메서드는 꽤나 복잡하기에, 중요 로직만 살펴보도록 하겠다.

실제 resize()메서드를 보면, newCap, newThr를 2배씩 증가시키는 것을 확인할 수 있다.
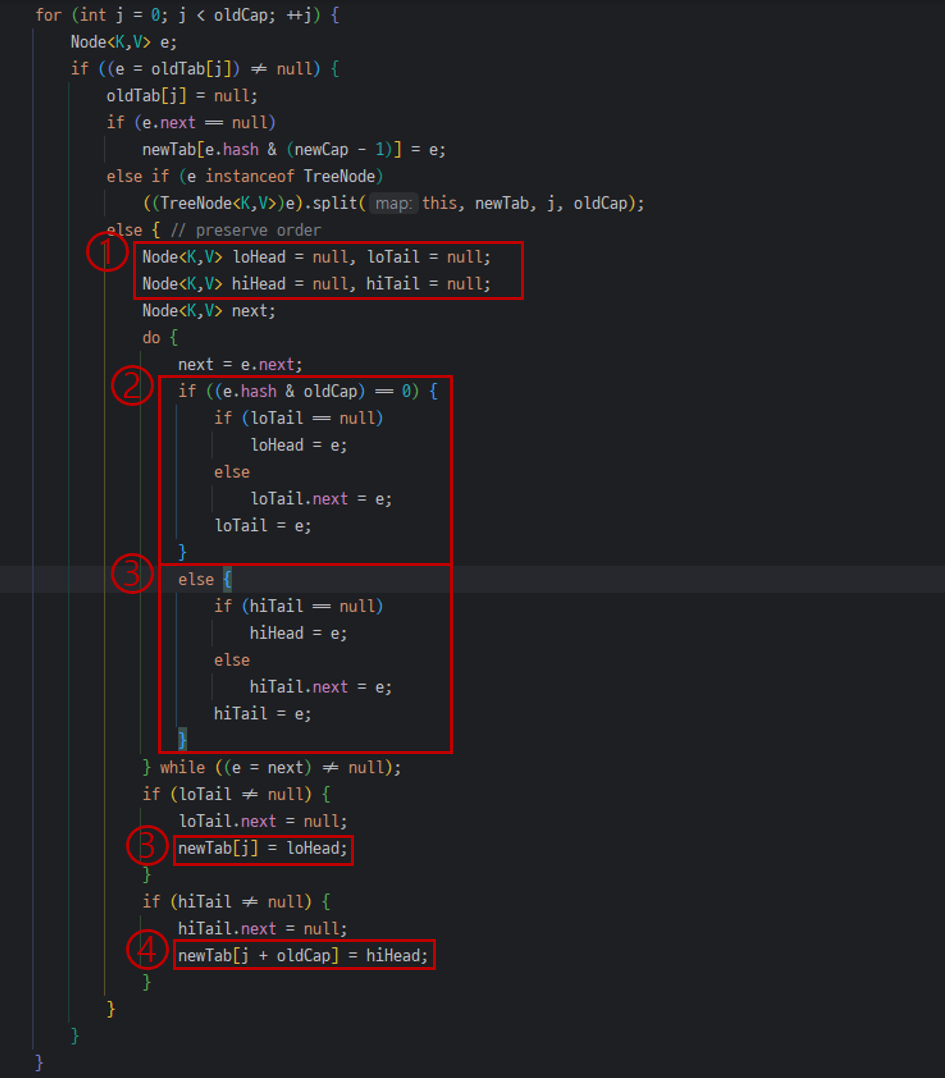
1번에서 loHead,loTail 과 hiHead,hiTail이 있다.
loHead/Tail은 현재 bucket index에 남아있을 요소들을 저장하는 링크드리스트가 된다.
hiHead/Tail은 index가 변경될 링크드 리스트가 된다.
그럼 index가 변경될지 여부를 결정하는 요소는 무엇일까?
아래 예시를 가지고 생각해보자.

5~20 hash값을 갖는 요소들은 모두 0번 index에 저장된다.
이때, 만약 bucket Size가 10으로 증가하면 어떻게 될까?

10번, 20번은 여전히 mod결과가 0이지만, 5번 15번은 mod결과가 5가되어 index를 이동해야한다.
이렇듯 절반은 기존 index에 남고 절반은 bucket을 이동해야함을 알 수 있다.
실제 코드에서 이를 판단하는 기준은 해당 부분이다.

e.hash & oldCap == 0 로직이 어떻게 이를 판단할 수 있는지 아래 예시로 다시 생각해보자.
| hash | hash(2진수) | oldCap(=16) | & 결과 | 이동 여부 |
| 16 | 0001 0000 | 0001 0000 | 0001 0000 | O |
| 32 | 0010 0000 | 0001 0000 | 0000 0000 | X |
| 48 | 0011 0000 | 0001 0000 | 0001 0000 | O |
| 64 | 0100 0000 | 0001 0000 | 0000 0000 | X |
| 80 | 0101 0000 | 0001 0000 | 0001 0000 | O |
| 96 | 0110 0000 | 0001 0000 | 0000 0000 | X |
| 112 | 0111 0000 | 0001 0000 | 0001 0000 | O |
| 128 | 1000 0000 | 0001 0000 | 0000 0000 | X |
위와같이 절반은 이동하지 않고 절반은 이동하는 형태가 된다.
이는 resizing이후 기존 데이터들이 균등하게 분산되도록 하는데 도움을 준다.
3-2. 2^n에서 오는 독특한 특성
"1-2. 나머지 연산을 &로 대신하기"에서 capacity가 2^n꼴이라는 점 때문에 나머지 연산을 &를 이용해 대체할 수 있음을 밝혔다.
index가 변경되어야 하는지를 판단할 때도 &를 이용했고 1:1로 균등하게 재배치가 되었다.
이또한 사실 capacity가 2^n 꼴이라 가능했던 것인데 이를 살펴보자.
capacity가 2^n꼴이 아닌 5라고 가정하면 아래와 같은 결과가 나온다.
| hash | hash(2진수) | oldCap(=5) | & 결과 | 이동 여부 |
| 5 | 0000 0101 | 0000 0101 | 0000 0101 | O |
| 10 | 0000 1010 | 0000 0101 | 0000 0000 | X |
| 15 | 0000 1111 | 0000 0101 | 0000 0101 | O |
| 20 | 0001 0100 | 0000 0101 | 0000 0100 | O |
| 25 | 0001 0101 | 0000 0101 | 0000 0000 | X |
| 30 | 0001 1110 | 0000 0101 | 0000 0100 | O |
| 35 | 0010 0101 | 0000 0101 | 0000 0101 | O |
| 40 | 0010 1000 | 0000 0101 | 0000 0000 | X |
아까와는 달리 이동여부가 1:1로 균등하게 재배치 되지 않는다.

oldCap는 2^4이므로 bit하나만 1을 가진다. 2배가 되면서 4번째 bit만 +1이 되다보니, 1과 0이 반복된다.
반면, oldCap가 5일때는 0000 0101로 표현됐다. 해당 패턴은 주기가 2보다 길어지는 현상이 나타나 1:1로 균등하게 분배되지 못했던 것이다.
3-3. 이젠 O(1)을 보장하나?
1. Red-Black Tree
2. Rehashing
두가지를 통해 hash Collision이 발생하더라도 최대한의 성능을 올리기 위해 노력한 흔적들이 보인다.
하지만, 당연하게도 O(1)을 보장하지는 못한다.
근본적으로, hash Collision의 확률을 줄이기 위해 hash()함수가 잘 정의되는 것이 중요하지 않을까 생각한다.
4. 31이라는 매직 넘버는 왜 자꾸 등장할까?
String은 어떻게 hashCode를 정의하고있을까?
// String의 hashCode()
public int hashCode() {
int h = hash;
if (h == 0 && !hashIsZero) {
h = isLatin1() ? StringLatin1.hashCode(value)
: StringUTF16.hashCode(value);
if (h == 0) {
hashIsZero = true;
} else {
hash = h;
}
}
return h;
}
// StringLatin1의 hashCode()
public static int hashCode(byte[] value) {
int h = 0;
for (byte v : value) {
h = 31 * h + (v & 0xff);
}
return h;
}
아래는 intelliJ를 통해 자동으로 생성한 hashCode()이다.
@Override
public int hashCode() {
int result = Objects.hashCode(name);
result = 31 * result + Objects.hashCode(brand);
result = 31 * result + price;
result = 31 * result + cnt;
return result;
}
ArrayList의 hashCode는 아래와 같다.
public int hashCode() {
int expectedModCount = modCount;
int hash = hashCodeRange(0, size);
checkForComodification(expectedModCount);
return hash;
}
int hashCodeRange(int from, int to) {
final Object[] es = elementData;
if (to > es.length) {
throw new ConcurrentModificationException();
}
int hashCode = 1;
for (int i = from; i < to; i++) {
Object e = es[i];
hashCode = 31 * hashCode + (e == null ? 0 : e.hashCode());
}
return hashCode;
}
3가지 클래스의 공통점은 무엇일까? 자세히 보면 31이라는 매직 넘버가 등장한다.
위 클래스들 뿐만 아니라 많은 클래스에서 hashCode를 정의할 때 31이라는 매직넘버가 등장한다.
31이라는 숫자가 무슨 의미를 가지기에 사용되는걸까?
31이라는 숫자가 절대적인 숫자는 아니라고 생각한다.
실제로 Lombok을 통해 생성된 hashCode를 보면 31이 아닌 다른 숫자를 이용한다.
@Generated
public int hashCode() {
int PRIME = 59;
int result = 1;
Object $orderDateTime = this.getOrderDateTime();
result = result * 59 + ($orderDateTime == null ? 43 : $orderDateTime.hashCode());
Object $beverages = this.getBeverages();
result = result * 59 + ($beverages == null ? 43 : $beverages.hashCode());
return result;
}
그럼 이는 아무 숫자나 상관없는 거냐 물어본다면 그렇지는 않다고 생각한다.
31이여야 하는 필연성은 없지만 여러 장점을 가진 숫자라고 생각한다.
짝수 보다는 홀수가 낫다.
상수가 32인 경우를 생각해보자.

hash결과에 32를 곱하는 것은 bit left shift 5칸을 하는것과 같다.
즉, 오른쪽에 0이 다섯개 붙는다.
우리는 곱하기 연산의 반복과 최종적인 나머지 연산을 통해 하위 bit들로 index를 찾아야한다.
이때, hash결과 하위 bit에 필연적으로 0이 붙어야 한다면 이는 무의미한 bit가 된다.
즉, hash collision의 확률이 증가한다.
상수가 k*2^n(n은 자연수)꼴로 나타난다면 하위 n bit가 0으로 고정된다는 것을 의미한다.
2^n꼴로 나타날 수 있는 수는 하위 bit를 무의미하게 만들기에 적절하지 못하다.
2^n - 1 꼴에 장점이 있다.
31 = 2^5 - 1의 꼴로 나타낼 수 있다.
곱하기가 CPU에서 처리될 때, 단순히 + 를 반복하는 것은 아니다.
bit shift 연산으로 최적화 할 수 있다면 이를 활용하는 방식으로 최적화 된다.
2^5 -1은 bit left shift 5를 한 후 -1을 하는 형태로 최적화 될 수 있다.
이는 다른 숫자에 비해 곱하기가 빠르게 처리될 수 있는있는 형태임을 의미한다.

너무 큰 수는 오버플로우의 위험이 있다.
hash()는 int(32bit 정수형)을 반환하는 함수이다.
상수가 너무 큰 숫자일 때, 오버플로우의 가능성이 있다.
유효한 bit들이 오버플로우로 사라지는 것은 hash collision의 확률을 높이는 길이기에 적당한 크기의 숫자가 필요했다.
정리
1. 적당한 크기의 숫자.
2. bit shift연산으로 최적화 하기 좋은 형태
3. 홀수
3가지 조건을 만족하는 적당한 숫자로 31이 자주 사용되는 것으로 보인다.
1-3에서 봤던 hash()메서드를 다시 한번 생각해보자
1-3에서 봤듯이 HashMap의 hash()메서드는 아래처럼 구현되어있다.
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
위 코드는 상위 bit와 하위 bit를 섞어줌으로써 상위 bit가 index결정에 영향을 주도록 하기 위함임을 설명했다.

곱하기 연산이 수행되고 나면 기존 hash가 가지고 있던 bit들이 상위 bit로 이동하게 되는것을 확인할 수 있다.
위에서 보던 31을 곱하는 함수는 Honer's method를 구현한 형태이다.

즉 반환되는 hashCode()의 형태는 위 연산의 결과를 따른다.(x=31)
31은 필드의 개수만큼 곱해지며 그때 마다 왼쪽으로 bit들이 이동할 것임을 예상할 수 있다.
이 때문에 상위 bit와 하위bit를 섞어주는 행위가 더 필요했던 것이 아닐까 생각한다.
hashCode()가 equals()보다 빠르다고?(삽질기)
hashCode와 equals중 hashCode가 왜 더 빠를까에 대해 고민하면서 String의 캐싱과 관련지어 고민했다.
지금은 이것이 핵심이 아니라는 것을 알고있지만, String의 캐싱에 대해서도 공유하고 싶은 마음과 작성한 글이 아까워 더보기로 공유한다 ㅎㅎ
HashMap에 대해서 찾아보다 보면 hashCode()가 equals()보다 더 빠르다는 이야기가 종종 보인다.
하지만, 가만히 생각해보면 이는 이상하게 들린다.
아래는 String의 hashCode()구현과 StringLatin1.hashCode()의 구현이다.
public int hashCode() {
int h = hash;
if (h == 0 && value.length > 0) {
hash = h = isLatin1() ? StringLatin1.hashCode(value)
: StringUTF16.hashCode(value);
}
return h;
}
public static int hashCode(byte[] value) {
int h = 0;
for (byte v : value) {
h = 31 * h + (v & 0xff);
}
return h;
}
위 구현을 보면 결국 byte마다 연산을 진행하여 int결과를 나타낸다.
각 byte를 ==으로 비교하는 것과 byte에 연산을 가한 뒤, 최종 값을 비교하는 것 중 후자가 더 빠르다는 것은 납득이 가지 않는다.
아래 간단한 테스트를 통해 이를 검증해 보았다.
문자열 생성은 apache.commons의 RandomStringUtils를 사용하였다.
package sample.cafekiosk.unit;
import org.apache.commons.lang3.RandomStringUtils;
import org.junit.jupiter.api.Test;
class HashCodeTest {
@Test
void hashCodeTest() {
String firstStr = RandomStringUtils.randomAlphabetic(1000);
String secondStr = RandomStringUtils.randomAlphabetic(1000);
hashStr(firstStr, secondStr);
equalsStr(firstStr, secondStr);
}
private void hashStr(final String firstStr, final String secondStr) {
long startTime = System.nanoTime();
boolean isEqual = false;
if (firstStr.hashCode() == secondStr.hashCode()) {
isEqual = true;
}
long endTime = System.nanoTime();
System.out.println("hashCode를 통해 연산하기" + (endTime - startTime) + " ns" + "(" + isEqual + ")");
}
private void equalsStr(final String firstStr, final String secondStr) {
long startTime = System.nanoTime();
boolean isEqual = false;
if (firstStr.equals(secondStr)) {
isEqual = true;
}
long endTime = System.nanoTime();
System.out.println("equals을 통해 연산하기" + (endTime - startTime) + " ns" + "(" + isEqual + ")");
}
}
아래는 출력 결과를 표로 정리한 것이다.
| 순번 | hashCode 결과 (ns) | equals 결과 (ns) | 더 빠른 경우 |
| 1 | 4000 | 1300 | equals |
| 2 | 4400 | 1300 | equals |
| 3 | 3200 | 1300 | equals |
| 4 | 4700 | 1600 | equals |
| 5 | 3100 | 1500 | equals |
| 6 | 4500 | 2100 | equals |
| 7 | 4900 | 1600 | equals |
| 8 | 4000 | 1400 | equals |
| 9 | 4100 | 1300 | equals |
| 10 | 3800 | 1800 | equals |
| 평균 | 4070 | 1520 | equals |
equals가 왜 더 빠른 결과가 나왔을까? equals의 내부 코드를 확인해보자.
@IntrinsicCandidate
public static boolean equals(byte[] value, byte[] other) {
if (value.length == other.length) {
for (int i = 0; i < value.length; i++) {
if (value[i] != other[i]) {
return false;
}
}
return true;
}
return false;
}
for문을 진행하는 과정에서 서로 다른 값이 나타나는 경우 바로 early termination을 시킨다.
이 때문에 equals는 문자열 전체를 탐색할 필요가 없는것이다.
여기까지 봤을 때, 적어도 String에 한해서 hashCode보다 equals가 명백히 빨라보인다.
그러면 hashCode가 equals보다 빠르다는 말은 어디서 나왔을까?
다시 String의 hashCode()구현을 확인해보자.
public int hashCode() {
int h = hash; // (1)
if (h == 0 && !hashIsZero) {
h = isLatin1() ? StringLatin1.hashCode(value)
: StringUTF16.hashCode(value);
if (h == 0) {
hashIsZero = true;
} else {
hash = h; // (2)
}
}
return h;
}
(1)에서 h 지역변수에 hash값을 넣어준다. 여기서 hash는 String이 가지고 있는 멤버 변수이다.
(2)에서 hash값에 대한 연산이 이뤄지고 나면 hash에 연산 결과를 캐싱해놓는다.
String은 hashCode 연산은 실질적으로 딱 한번만 이뤄지고 이후부터는 캐싱된 결과를 바로 반환하는 것이다.
일반적인 객체의 hashCode와 equals의 구현에 대해 생각해보자.
intelliJ를 통해 자동으로 생성한 hashCode와 equals에 대한 구현 코드이다.
import java.util.Objects;
public class Americano {
public String name;
public String brand;
public int price;
public int cnt;
public Americano(final String name, final String brand, final int price, final int cnt) {
this.name = name;
this.brand = brand;
this.price = price;
this.cnt = cnt;
}
@Override
public boolean equals(final Object o) {
if (o == null || getClass() != o.getClass()) return false;
final Americano americano = (Americano) o;
return price == americano.price && cnt == americano.cnt && Objects.equals(name, americano.name) && Objects.equals(brand, americano.brand);
}
@Override
public int hashCode() {
int result = Objects.hashCode(name);
result = 31 * result + Objects.hashCode(brand);
result = 31 * result + price;
result = 31 * result + cnt;
return result;
}
}
잘 생각해보면 우리가 다루는 객체들은 대부분 문자열과 숫자로 이루어져있다.
객체 내부에 다른 객체를 가지거나 배열 컬렉션을 가지더라도 그또한 모두 문자열과 숫자의 집합이다.
이 중 연산이 오래걸리는 String이 캐싱되어 있어 값을 그대로 반환할 수 있다면 평균적으로 hashCode가 equals보다 더 빠르게 처리된다는 말도 납득이 된다. hashCode가 equals보다 더 빠르게 처리된다는 말은 여기서 나온 것이 아닐까 생각된다.
* Object.hashCode는 내부에서 null체크 후 파라미터로 전달된 객체의 hashCode를 호출하는 메서드이다.
왜 String만 hashCode를 캐싱하지?
캐싱을 통해 hashCode의 반환 속도를 높일 수 있다면 아래와 같이 hashCode를 캐싱해주는 것이 더 좋지 않을까?
import java.util.Objects;
public class Americano {
public String name;
public String brand;
public int price;
public int cnt;
public Integer hash = null;
public Americano(final String name, final String brand, final int price, final int cnt) {
this.name = name;
this.brand = brand;
this.price = price;
this.cnt = cnt;
}
@Override
public boolean equals(final Object o) {
if (o == null || getClass() != o.getClass()) return false;
final Americano americano = (Americano) o;
return price == americano.price && cnt == americano.cnt && Objects.equals(name, americano.name) && Objects.equals(brand, americano.brand);
}
@Override
public int hashCode() {
Integer h = hash;
if(h == null){
h = Objects.hashCode(name);
h = 31 * h + Objects.hashCode(brand);
h = 31 * h + price;
h = 31 * h + cnt;
}
return h;
}
}
하지만 Lombok이나 IntelliJ와 같은 도구를 통해 자동으로 생성해주는 hashCode는 저런식으로 구현되지 않는다.
이유는 불변성에 있다고 생각한다.
String은 Immutable한 객체이다. 값이 변경되는 것이 구조적으로 불가능하다.
하지만 우리가 작성한 클래스는 mutable한 객체이다.
따라서 hash가 캐싱된 상태에서 값이 변경될 경우 복잡한 상황이 발생할 수 있다.
이러한 부분을 고려하여 hashCode를 캐싱하지 않는 형태로 코드를 생성해주는 것 같다.
불변성으로 설계된 클래스는 위 처럼 hashCode를 정의할 수도 있겠지만, 실제로 HashMap에서는 hash가 한번만 호출되므로 유의미한 차이가 나는 경우는 잘 없을 것으로 생각된다.
'알고리즘&자료구조' 카테고리의 다른 글
| 삽입 정렬(Insertion Sort) (1) | 2023.01.01 |
|---|---|
| 선택 정렬(Selection Sort) (0) | 2022.12.31 |